Fzero matlab не работает

Иллюстрированный самоучитель по MatLab

Вычисление нулей функции одной переменной

Ряд функций системы MATLAB предназначен для работы с функциями. По аналогии с дескрипторами графических объектов могут использоваться объекты класса дескрипторов функций, задаваемых с помощью символа @, например:

Примечание
Подфункциями понимаются как встроенные функции, например sin(x) или ехр(х),так и функции пользователя, например f(x), задаваемые как т-файлы-функции.

Численные значения таких функций, заданных дескрипторами, вычисляются с помощью функции feval:

Для совместимости с прежними версиями можно записывать функции в символьном виде в апострофах, использование функции eval для их вычисления может быть более наглядно, не нужно создавать m-файл, но в учебном курсе мы будем стараться использовать новую нотацию, с использованием дескрипторов функций и feval, так как при этом программирование становится «более объектно-ориентированным», повышается скорость, точность и надежность численных методов. Поэтому, хотя везде в нижеследующем тексте вместо @fun можно подставить и символьное значение функции в апострофах, мы будем использовать нотацию @fun в дидактических целях. Все же иногда в интерактивном режиме можно использовать старую запись, чтобы не создавать m-файл функции.

Довольно часто возникает задача решения нелинейного уравнения вида f(x) = 0 или /, (г) =/ ₂ (дг). Последнее, однако, можно свести к виду f(x) =f ₁ (х) – f ₂ (х) = 0. Таким образом, данная задача сводится к нахождению значений аргумента х функции f(x) одной переменной, при котором значение функции равно нулю. Соответствующая функция MATLAB, решающая данную задачу, приведена ниже:

• fzero(@fun,x) – возвращает уточненное значение х, при котором достигается нуль функции fun, представленной в символьном виде, при начальном значении аргумента х. Возвращенное значение близко к точке, где функция меняет знак, или равно NaN, если такая точка не найдена;
• fzero(@fun,[x1 x2]) – возвращает значение х, при котором fun(x)=0 с заданием интервала поиска с помощью вектора x=[xl х2], такого, что знак fun(x(D) отличается от знака fun(x(2)). Если это не так, выдается сообщение об ошибке. Вызов функции fzero с интервалом гарантирует, что fzero возвратит значение, близкое к точке, где fun изменяет знак;
• fzero(@fun,x.tol) – возвращает результат с заданной погрешностью tol;
• fzero(@fun,x.tol.trace) – выдает на экран информацию о каждой итерации;
• fzero(@fun,х.tol.trace,Р1.Р2,…) – предусматривает дополнительные аргументы, передаваемые в функцию fun(x.Pl,P2,…). При задании пустой матрицы для tol или trace используются значения по умолчанию. Пример:

Для функции fzero ноль рассматривается как точка, где график функции fun пересекает ось х, а не касается ее. В зависимости от формы задания функции fzero реализуются следующие хорошо известные численные методы поиска нуля функции: деления отрезка пополам, секущей и обратной квадратичной интерполяции. Приведенный ниже пример показывает приближенное вычисление р/2 из решения уравнения cos(x)=0 с представлением косинуса дескриптором:

В более сложных случаях настоятельно рекомендуется строить график функции f(x) для приближенного определения корней и интервалов, в пределах которых они находятся. Ниже дан пример такого рода (следующий листинг представляет собой содержимое m-файла fun1.m):

Из рисунка нетрудно заметить, что значения корней заключены в интервалах [0.5 1], [2 3] и [5 6]. Найдем их, используя функцию fzero:

Обратите внимание на то, что корень х3 найден двумя способами и что его значения в третьем знаке после десятичной точки отличаются в пределах заданной погрешности tol =0.001. К сожалению, сразу найти все корни функция fzero не в состоянии. Решим эту же систему при помощи функции fsolve из пакета Optimization Toolbox, которая решает систему нелинейных уравнений вида f(x)=0 методом наименьших квадратов, ищет не только точки пересечения, но и точки касания, fsolve имеет почти те же параметры (дополнительный параметр – задание якобиана) и почти ту же запись, что и функция lsqnonneg, подробно рассмотренная ранее. Пример:

Для решения систем нелинейных уравнений следует также использовать функцию solve из пакета Symbolic Math Toolbox. Эта функция способна выдавать результат в символьной форме, а если такого нет, то она позволяет получить решение в численном виде. Пример:

[Пакеты расширения Symbolic Math ToolBox и Extended Symbolic Math Toolbox MATLAB 6.0 используют ядро Maple V Release 5 35 и являются поэтому исключением: они пока не поддерживают новую нотацию с использованием дескрипторов функций. – Примеч. ред.]

Источник

fzero

Root of nonlinear function

Syntax

Description

x = fzero( fun , x0 ) tries to find a point x where fun(x) = 0 . This solution is where fun(x) changes sign— fzero cannot find a root of a function such as x^2 .

x = fzero( fun , x0 , options ) uses options to modify the solution process.

x = fzero( problem ) solves a root-finding problem specified by problem .

[ x , fval , exitflag , output ] = fzero( ___ ) returns fun(x) in the fval output, exitflag encoding the reason fzero stopped, and an output structure containing information on the solution process.

Examples

Root Starting From One Point

Calculate π by finding the zero of the sine function near 3 .

Root Starting From an Interval

Find the zero of cosine between 1 and 2 .

Note that cos ( 1 ) and cos ( 2 ) differ in sign.

Root of a Function Defined by a File

Find a zero of the function f( x) = x 3 – 2 x – 5.

First, write a file called f.m .

Save f.m on your MATLAB ® path.

Find the zero of f( x) near 2 .

Since f(x) is a polynomial, you can find the same real zero, and a complex conjugate pair of zeros, using the roots command.

Root of Function with Extra Parameter

Find the root of a function that has an extra parameter.

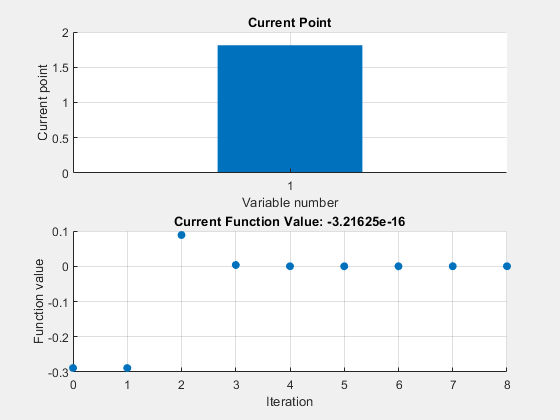
Nondefault Options

Plot the solution process by setting some plot functions.

Define the function and initial point.

Examine the solution process by setting options that include plot functions.

Run fzero including options .

Solve Problem Structure

Solve a problem that is defined by a problem structure.

Define a structure that encodes a root-finding problem.

Solve the problem.

More Information from Solution

Find the point where exp(-exp(-x)) = x , and display information about the solution process.

fval = 0 means fun(x) = 0 , as desired.

Input Arguments

fun — Function to solve
function handle | function name

Function to solve, specified as a handle to a scalar-valued function or the name of such a function. fun accepts a scalar x and returns a scalar fun(x) .

fzero solves fun(x) = 0 . To solve an equation fun(x) = c(x) , instead solve fun2(x) = fun(x) — c(x) = 0 .

To include extra parameters in your function, see the example Root of Function with Extra Parameter and the section Parameterizing Functions.

Example: ‘sin’

Example: @myFunction

Example: @(x)(x-a)^5 — 3*x + a — 1

Data Types: char | function_handle | string

x0 — Initial value
scalar | 2-element vector

Initial value, specified as a real scalar or a 2-element real vector.

Scalar — fzero begins at x0 and tries to locate a point x1 where fun(x1) has the opposite sign of fun(x0) . Then fzero iteratively shrinks the interval where fun changes sign to reach a solution.

2-element vector — fzero checks that fun(x0(1)) and fun(x0(2)) have opposite signs, and errors if they do not. It then iteratively shrinks the interval where fun changes sign to reach a solution. An interval x0 must be finite; it cannot contain ± Inf .

Tip

Calling fzero with an interval ( x0 with two elements) is often faster than calling it with a scalar x0 .

Источник

fzero

Root of nonlinear function

Syntax

Description

x = fzero( fun , x0 ) tries to find a point x where fun(x) = 0 . This solution is where fun(x) changes sign— fzero cannot find a root of a function such as x^2 .

x = fzero( fun , x0 , options ) uses options to modify the solution process.

x = fzero( problem ) solves a root-finding problem specified by problem .

[ x , fval , exitflag , output ] = fzero( ___ ) returns fun(x) in the fval output, exitflag encoding the reason fzero stopped, and an output structure containing information on the solution process.

Examples

Root Starting From One Point

Calculate π by finding the zero of the sine function near 3 .

Root Starting From an Interval

Find the zero of cosine between 1 and 2 .

Note that cos ( 1 ) and cos ( 2 ) differ in sign.

Root of a Function Defined by a File

Find a zero of the function f( x) = x 3 – 2 x – 5.

First, write a file called f.m .

Save f.m on your MATLAB ® path.

Find the zero of f( x) near 2 .

Since f(x) is a polynomial, you can find the same real zero, and a complex conjugate pair of zeros, using the roots command.

Root of Function with Extra Parameter

Find the root of a function that has an extra parameter.

Nondefault Options

Plot the solution process by setting some plot functions.

Define the function and initial point.

Examine the solution process by setting options that include plot functions.

Run fzero including options .

Solve Problem Structure

Solve a problem that is defined by a problem structure.

Define a structure that encodes a root-finding problem.

Solve the problem.

More Information from Solution

Find the point where exp(-exp(-x)) = x , and display information about the solution process.

fval = 0 means fun(x) = 0 , as desired.

Input Arguments

fun — Function to solve
function handle | function name

Function to solve, specified as a handle to a scalar-valued function or the name of such a function. fun accepts a scalar x and returns a scalar fun(x) .

fzero solves fun(x) = 0 . To solve an equation fun(x) = c(x) , instead solve fun2(x) = fun(x) — c(x) = 0 .

To include extra parameters in your function, see the example Root of Function with Extra Parameter and the section Parameterizing Functions.

Example: ‘sin’

Example: @myFunction

Example: @(x)(x-a)^5 — 3*x + a — 1

Data Types: char | function_handle | string

x0 — Initial value
scalar | 2-element vector

Initial value, specified as a real scalar or a 2-element real vector.

Scalar — fzero begins at x0 and tries to locate a point x1 where fun(x1) has the opposite sign of fun(x0) . Then fzero iteratively shrinks the interval where fun changes sign to reach a solution.

2-element vector — fzero checks that fun(x0(1)) and fun(x0(2)) have opposite signs, and errors if they do not. It then iteratively shrinks the interval where fun changes sign to reach a solution. An interval x0 must be finite; it cannot contain ± Inf .

Tip

Calling fzero with an interval ( x0 with two elements) is often faster than calling it with a scalar x0 .

Источник

Документация

Корень нелинейной функции

Синтаксис

Описание

x = fzero( fun , x0 ) попытки найти точку x где fun(x) = 0 . Это решение состоит в том где fun(x) изменяет знак — fzero не может найти корень функции, такой как x^2 .

x = fzero( fun , x0 , options ) использование options изменить процесс решения.

x = fzero( problem ) решает находящую корень задачу, заданную problem .

[ x , fval , exitflag , output ] = fzero( ___ ) возвращает fun(x) в fval выведите, exitflag кодирование причины fzero остановленный, и структура output, содержащая информацию о процессе решения.

Примеры

Корень, начинающий с одной точки

Вычислить π путем нахождения нуля синусоидальной функции около 3 .

Корень, начинающий с интервала

Найдите нуль косинуса между 1 и 2 .

Обратите внимание на то, что cos ( 1 ) и cos ( 2 ) отличайтесь по знаку.

Корень функции, определяемой файлом

Найдите нуль функционального f ( x) = x 3 – 2 x – 5.

Во-первых, запишите файл под названием f.m .

Сохраните f.m на вашем MATLAB ® path.

Найдите нуль f ( x) около 2 .

Начиная с f(x) полином, можно найти тот же действительный нуль и комплексно-сопряженную пару нулей, с помощью roots команда.

Корень функции с дополнительным параметром

Найдите корень функции, которая имеет дополнительный параметр.

Опции не по умолчанию

Постройте процесс решения путем установки некоторых функций построения графика.

Задайте функциональную и начальную точку.

Исследуйте процесс решения путем установки опций, которые включают функции построения графика.

Запустите fzero включая options .

Решение проблемной структуры

Решите задачу, которая описана структурой задачи.

Задайте структуру, которая кодирует находящую корень проблему.

Больше информации из решения

Найдите точку где exp(-exp(-x)) = x , и отобразите информацию о процессе решения.

fval = 0 средних значений fun(x) = 0 , как желаемый.

Входные параметры

fun — Функция, чтобы решить
указатель на функцию | имя функции

Функция, чтобы решить в виде указателя на скалярную функцию или имя такой функции. fun принимает скалярный x и возвращает скалярный fun(x) .

fzero решает fun(x) = 0 . Решить уравнение fun(x) = c(x) , вместо этого решите fun2(x) = fun(x) — c(x) = 0 .

Чтобы включать дополнительные параметры в вашу функцию, смотрите Корень в качестве примера Функции Дополнительным Параметром и разделом Parameterizing Functions.

Пример: ‘sin’

Пример: @myFunction

Пример: @(x)(x-a)^5 — 3*x + a — 1

Типы данных: char | function_handle | string

x0 — Начальное значение
скаляр | вектор с 2 элементами

Начальное значение в виде действительного скаляра или вектора действительных чисел с 2 элементами.

Скаляр — fzero начинается в x0 и попытки определить местоположение точки x1 где fun(x1) имеет противоположный знак fun(x0) . Затем fzero итеративно уменьшает интервал где fun изменяет знак, чтобы достигнуть решения.

Вектор с 2 элементами — fzero проверки, что fun(x0(1)) и fun(x0(2)) имейте противоположные знаки и ошибки, если они не делают. Это затем итеративно уменьшает интервал где fun изменяет знак, чтобы достигнуть решения. Интервал x0 mustBeFinite; это не может содержать ± Inf .

Совет

Вызов fzero с интервалом ( x0 с двумя элементами), часто быстрее, чем вызов его со скалярным x0 .

Пример 3

Пример: [2,17]

Типы данных: double

options — Опции для процесса решения
структура, обычно созданное использование optimset

Опции для процесса решения в виде структуры. Создайте или измените options использование структуры optimset fzero использование они options поля структуры.

Level of display:

‘off’ не отображает вывода.

‘iter’ отображает вывод в каждой итерации.

‘final’ отображения только окончательный результат.

‘notify’ (значение по умолчанию) отображает вывод, только если функция не сходится.

Проверяйте, допустимы ли значения целевой функции.

‘on’ отображает ошибку, когда целевая функция возвращает значение, которое является complex Inf , или NaN .

Значение по умолчанию, ‘off’ , отображения никакая ошибка.

Задайте одну или несколько пользовательских функций, которые оптимизационная функция вызывает на каждой итерации, или как указатель на функцию или как cell-массив указателей на функцию. Значение по умолчанию не ни один ( [] ). Смотрите выходные функции решателя оптимизации.

Постройте различные показатели прогресса, в то время как алгоритм выполняется. Выберите из предопределенных графиков или запишите свое собственное. Передайте указатель на функцию или cell-массив указателей на функцию. Значение по умолчанию не ни один ( [] ).

@optimplotx строит текущую точку.

@optimplotfval строит значение функции.

Для получения информации о записи пользовательской функции построения графика смотрите Функции построения графика Решателя Оптимизации.

Допуск завершения на x , положительная скалярная величина. Значением по умолчанию является eps , 2.2204e–16.

Пример: options = optimset(‘FunValCheck’,’on’)

Типы данных: struct

problem — Находящая корень проблема
структура

Находящая корень проблема в виде структуры со всеми следующими полями.

Начальная точка для x , действительный скалярный или вектор с 2 элементами

Структура опций, обычно созданное использование optimset

Типы данных: struct

Выходные аргументы

x — Местоположение корня или изменения знака
действительный скаляр

Местоположение корня или изменения знака, возвращенного как скаляр.

fval — Значение функции в x
действительный скаляр

Значение функции в x , возвращенный как скаляр.

exitflag — Целое число, кодирующее выходное условие
целое число

Целое число, кодирующее выходное условие, означая причину fzero остановленный его итерации.

Функция сходилась к решению x .

Алгоритм был отключен выходной функцией или функцией построения графика.

NaN или Inf со значением функции столкнулись при поиске интервала, содержащего изменение знака.

Со значением комплексной функции столкнулись при поиске интервала, содержащего изменение знака.

Алгоритм может сходиться к особой точке.

fzero не обнаружил изменение знака.

output — Информация о находящем корень процессе
структура

Информация о находящем корень процессе, возвращенном как структура. Поля структуры:

Количество проделанных итераций, чтобы найти интервал, содержащий корень

Количество находящих нуль итераций

Количество вычислений функции

Алгоритмы

fzero команда является файлом функции. Алгоритм, созданный Т. Деккером, использует комбинацию деления пополам, секанса и обратных квадратичных методов интерполяции. Алгол 60 версий, с некоторыми улучшениями, дан в [1]. Версия Фортрана, на который fzero базируется, находится в [2].

Альтернативная функциональность

Приложение

Оптимизировать задача Live Editor обеспечивает визуальный интерфейс для fzero .

Ссылки

[1] Брент, R., алгоритмы для минимизации без производных, Prentice Hall, 1973.

[2] Форсайт, G. E. М. А. Малкольм, и К. Б. Молер, компьютерные методы для математических вычислений, Prentice Hall, 1976.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Для генерации кода C/C++:

fun входной параметр должен быть указателем на функцию, и не структурой или вектором символов.

fzero игнорирует все опции за исключением TolX и FunValCheck .

fzero не поддерживает четвертый выходной аргумент, структуру output.

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool .

Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.

Смотрите также

Открытый пример

У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?

Документация MATLAB

Поддержка

© 1994-2021 The MathWorks, Inc.

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста — например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

Источник