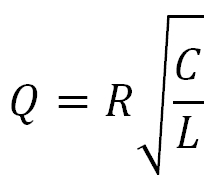Как настроить резонансный контур

Параллельный колебательный контур

В прошлой статье мы с вами рассмотрели последовательный колебательный контур, так как все участвующие в нем радиоэлементы соединялись последовательно. В этой же статье мы рассмотрим параллельный колебательный контур, в котором катушка и конденсатор соединяются параллельно.

Параллельный колебательный контур

Идеальный колебательный контур

На схеме идеальный колебательный контур выглядит вот так:

L — индуктивность, Генри

С — емкость, Фарад

Реальный колебательный контур

В реальности у нас катушка обладает приличным сопротивлением потерь, так как намотана из провода, да и конденсатор тоже имеет некоторое сопротивление потерь. Потери в емкости очень малы и ими обычно пренебрегают. Поэтому оставим только одно сопротивление потерь катушки R. Тогда схема реального колебательного контура примет вот такой вид:

R — это сопротивление потерь контура, Ом

L — индуктивность, Генри

С — емкость, Фарад

Принцип работы параллельного колебательного контура

Давайте подцепим к генератору частоты реальный параллельный колебательный контур

Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.

Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.

Реактивное сопротивление катушки выражается по формуле

а конденсатора по формуле

Более подробно про это можно прочитать в этой статье.

Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки X_L и конденсатора X_C уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.

Резонанс параллельного колебательного контура

Очень интересное свойство параллельного колебательного контура заключается в том, что при Х_L = Х_С у нас колебательный контур войдет в резонанс. При резонансе колебательный контур начнет оказывать большее сопротивление переменному электрическому току. Еще часто это сопротивление называют резонансным сопротивлением контура и оно выражается формулой:

R_рез — это сопротивление контура на резонансной частоте

L — собственно сама индуктивность катушки

C — собственно сама емкость конденсатора

R — сопротивление потерь катушки

Формула резонанса

Для параллельного колебательного контура также работает формула Томсона для резонансной частоты как и для последовательного колебательного контура:

F — это резонансная частота контура, Герцы

L — индуктивность катушки, Генри

С — емкость конденсатора, Фарады

Как найти резонанс параллельного колебательного контура на практике

Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.

Итак, реальная схема этого контура будет вот такая:

Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:

На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.

Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура R_кон.

Упрощенная схема будет выглядеть вот так:

Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление R_кон будет максимальным, вследствие чего у нас на этом сопротивлении «упадет» бОльшее напряжение.

Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.

Как вы видите, на колебательном контуре «падает» малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление R_кон

Добавляем частоту. 11,4 Килогерца

Как вы видите, напряжение на контуре поднялось. Это значит, что сопротивление колебательного контура увеличилось.

Добавляем еще частоту. 50 Килогерц

Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.

Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик. Напряжение выросло, так как сопротивление колебательного контура стало еще больше.

И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре. Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам.

Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:

Снова добавляем частоту и видим, что напряжение стало еще меньше:

Что происходит на резонансной частоте в параллельном колебательном контуре

Давайте более подробно рассмотрим эту осциллограмму, когда у нас было максимальное напряжение с контура.

Что здесь у нас произошло?

Так как на этой частоте был всплеск напряжения, следовательно, на этой частоте параллельный колебательный контур имел самое высокое сопротивление R_кон. На этой частоте Х_L = Х_С. Потом с ростом частоты сопротивление контура снова упало. Это и есть то самое резонансное сопротивление контура, которое выражается формулой:

Резонанс токов

Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:

Чему будет равняться резонансный ток I_рез ? Считаем по закону Ома:

Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток I_кон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.

Добротность параллельного колебательного контура

Кстати, этот контурный ток будет намного больше, чем ток, который проходит через контур. И знаете во сколько раз? Правильно, в Q раз. Q — это и есть добротность! В параллельном колебательном контуре она показывает во сколько раз сила тока в контуре I_кон больше сила тока в общей цепи I_рез

Если сюда еще прилепить сопротивление потерь, то формула примет вот такой вид:

R — сопротивление потерь на катушке, Ом

Применение параллельного колебательного контура

Параллельный колебательный контур применяется в радиоприемном оборудовании, где надо выделить частоту какой-либо станции. Также с помощью колебательного контура можно построить различные резонансные фильтры.

Источник

Вынужденные колебания. Резонанс. Амплитуда и фаза вынужденных колебаний

Настройка контура

Для плавной настройки приемника обычно используется конденсатор переменной емкости (лист 92). Такой конденсатор состоит из двух частей: неподвижной — статора и подвижной — ротора. Статор и ротор собраны из тонких пластин, причем ротор соединен с металлическим корпусом конденсатора, а статор изолирован от него. Большое число пластин необходимо для того, чтобы получить сравнительно большую емкость при небольших габаритах конденсатора. При монтаже ротор, как правило, соединяют с нижним (по схеме) концом катушки, то есть фактически заземляют. При повороте ротора изменяется расстояние между его пластинами и пластинами статора, а вместе с этим изменяется и емкость конденсатора. Основной характеристикой таких конденсаторов является максимальная емкость Смакс (пластины полностью введены) и минимальная емкость Смин (пластины полностью выведены). На схемах указываются обе эти величины (через тире).

Широкое распространение получили стандартные блоки, состоящие из двух конденсаторов переменной емкости (двух секций), каждый из которых имеет максимальную емкость Смакс = 450 (520) пф и минимальную Смин= 15 (25) пф. Роторы обеих секций соединены между собой, так как они закреплены на общей металлической оси. На схеме конденсаторы, роторы которых закреплены на одной оси, соединяют пунктирной линией. В случае необходимости, например в детекторном приемнике, можно использовать только одну секцию блока, не подключая никуда статор второй секции.

С помощью одного конденсатора стандартного блока можно плавно изменять частоту настройки контура в три-четыре раза и таким образом полностью перекрыть один из радиовещательных диапазонов. При этом максимальной емкости будет соответствовать самая низкая частота диапазона, а минимальной емкости — самая высокая частота. Это следует из рассмотренной нами основной формулы для f: с увеличением емкости конденсатора резонансная частота контура уменьшается.

Для перехода с одного диапазона на другой в контуре осуществляется переключение катушек. Так, например, для перехода с длинных волн на средние индуктивность катушки Lк уменьшают примерно в десять раз, а при переходе на короткие волны — еще в десять-двадцать раз. Конденсатор настройки на всех диапазонах используется один и тот же, а катушки к нему подключаются с помощью переключателя (переключатель диапазонов, рис. 56).

Для того чтобы при налаживании приемника можно было точно подогнать границы диапазона, в контур вводят элементы подстройки. Один из этих элементов — это подключенный непосредственно к катушке, а следовательно, определяющий общую емкость контура, подстроечный конденсатор Сп (лист 93), емкость которого можно изменять от 5-10 до 25-30 пф. Этот конденсатор (его иногда называют «триммер») особенно сильно влияет на настройку контура на самых высоких частотах, когда ротор конденсатора настройки выведен. Это объясняется тем, что подстроечный конденсатор фактически подключен параллельно конденсатору настройки Ск, и общая емкость контура определяется их суммой.

Когда емкость конденсатора настройки Ск мала, то даже небольшие изменения емкости Сп оказываются весьма ощутимыми. Если же полностью ввести ротор конденсатора Ск, то на фоне его большой емкости влияние Сп будет незначительным. Сказанное хорошо иллюстрируется простым примером. Допустим, что емкость Ск изменяется от 20 пф до 500 пф, а емкость Сп можно менять в пределах 5-30 пф. При выведенном роторе конденсатора настройки (Ск=20 пф) общую емкость контура можно менять с помощью Сп от 25 пф (20+5) до 50 пф (20+30), то есть в два раза. Когда же мы введем ротор (Ск=500 пф), то общую емкость контура можно будет менять лишь на 5% — от 505 пф (500+5) до 530 пф (500+30). Поэтому мы и говорим, что в основном Сп влияет на резонансную частоту контура на самых высоких частотах диапазона, то есть при минимальной емкости конденсатора Ск (рис. 57, 58).

Вынужденные колебания. Резонанс. Амплитуда и фаза вынужденных колебаний

Рассмотрим колебания, которые поддерживаются в системе внешней гармонической силой F

=
F
0Cosw
t
. Такие колебания называются вынужденными.

Обратимся вновь к пружинному маятнику. Вспомним уравнения движения этого осциллятора:

— уравнение собственных незатухающих колебаний. В системе действует одна упругая сила F

— собственные затухающие колебания. В системе появилась сила вязкого сопротивления, пропорциональная скорости .

В случае вынужденных колебаний кроме двух названных сил — упругой и силы сопротивления, на систему действует ещё одна сила: F

— дифференциальное уравнение вынужденных колебаний пружинного маятника. Это уравнение движения принято записывать так:

Введя знакомые обозначения и , представим уравнение движения осциллятора окончательно в таком виде:

Опыт показывает, что под действием гармонического возмущающего усилия F

=
F
0Cosw
t
осциллятор совершает гармонические колебания с частотой вынуждающей силы w:

Если частота w известна, то задача сводится к определению амплитуды вынужденных колебаний А

и начальной фазы a.

Продифференцировав функцию (13.15), подставим ее в уравнение (13.14):

Теперь воспользуемся известными тригонометрическими формулами для косинуса и синуса суммы двух углов:

Это уравнение представляет собой сумму двух гармонических слагаемых

Последнее равенство возможно в единственном случае, если постоянные во времени a

и
b
равны нулю:
а
= 0,
b
= 0. Это означает, что справедливы следующие уравнения:

Эти два уравнения содержат только две неизвестные величины: амплитуду А

и фазу a вынужденного колебания. Для отыскания амплитуды
А
можно домножить уравнение (13.16) на , а уравнение (13.17) — на Cosa. Вычтя теперь из первого уравнения второе, получим Sina:

Воспользовавшись этим результатом в уравнении (13.17), найдем Cosa:

Возведем уравнения (13.18) и (13.19) в квадрат и сложим:

Последнее уравнение решим относительно искомой амплитуды колебаний А

Фазовый сдвиг смещения x

относительно возмущающего усилия
F
найдём непосредственно из уравнения (13.17):

Обратимся к анализу полученных результатов.

1) Амплитуда вынужденных колебаний прямо пропорциональна амплитуде возмущающего усилия F

2) Если w = 0 — случай приложения статической нагрузки F

0, смещение груза будет определяться жёсткостью пружины k:

3) При высоких частотах внешнего усилия (w→¥), амплитуда колебаний А

4) Для отыскания частоты wрез, при которой амплитуда достигает наибольшего значения А

рез, нужно найти минимум выражения, стоящего под корнем в знаменателе уравнения (13.20). Продифференцировав это выражение по w, и приравняв результат нулю, получим условие, определяющее wрез:

Отсюда следует, что резонансная частота wрез меньше частоты собственных незатухающих колебаний w0:

Используя это значение в (13.20), рассчитаем резонансную амплитуду:

5) Если вязкое сопротивление отсутствует, коэффициент затухания d = = 0 и резонансная амплитуда устремляется в бесконечность. При этом условии резонансная частота, как следует из (13.22), равна частоте собственных незатухающих колебаний осциллятора wрез = w0.

6) С увеличением коэффициента затухания d, резонансная частота и амплитуда колебаний уменьшаются.

Все эти закономерности графически представлены на рис. 13.4.

7) При слабом затухании, когда , резонансная амплитуда равна

Разделим это выражение на — смещение под действием постоянной силы:

Таким образом, добротность осциллятора численно равна отношению резонансной амплитуды к смещению под действием постоянной силы.

На рис. 13.5 представлена зависимость фазового сдвига вынужденных колебаний и вынуждающей силы — график функции (13.21). С увеличением частоты вынуждающего усилия a растет, меняясь от 0 до p. В резонансе фазовый сдвиг равен . Эта зависимость a = a(w) меняется с изменением коэффициента затухания.

Лекция 14 «Элементы специальной теории относительности»

1. Постулаты специальной теории относительности. Преобразования Лоренца.

2. Динамика релятивистского движения.

3. Закон эквивалентности массы и энергии.

АльбертЭйнштейн

В классической механике Ньютона мы изучали законы движения макротел со скоростями, далекими от скорости света (с
= 3 × 108 м/с). Такие движения называются нерелятивистскими (классическими), в отличие от релятивистских движений, скорость которых соизмерима со скоростью света. Теоретической основой релятивистской механики является специальная (частная) теория относительности (СТО). Предваряя рассмотрение основных положений этой теории, отметим два важных момента:

1) Релятивистская механика включает в себя и классическую механику как предельный случай движения с малыми скоростями.

2) Все положения СТО имеют сегодня надежное экспериментальное подтверждение.

Колебательный контур LC

— электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

– реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию. — Катушка индуктивности
L
– реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Резонанс

Если схема с конденсатором, катушкой и резистором возбуждается напряжением, постоянно меняющимся во времени с определенной частотой, то также изменяются реактивные сопротивления: индуктивное и емкостное. Амплитуда и частота выходного сигнала будет изменяться по сравнению с входным.

Частота вращения: формула

Индуктивное сопротивление прямо пропорционально частоте:

а емкостное сопротивление обратно пропорционально этому показателю:

X(C) = 1/(2π x f x C).

Важно! На более низких частотах индуктивное сопротивление незначительное, а емкостное будет высоким и сможет создавать практически разомкнутый контур. На высоких частотах картина обратная.

При конкретной комбинации конденсатора и катушки схема становится резонансной, или настроенной, имеющей частоту колебаний, при которой индуктивное сопротивление идентично емкостному. И они компенсируют друг друга.

Следовательно, в цепи остается исключительно активное сопротивление, противостоящее протекающему току. Созданные условия получили наименование резонанса колебательного контура. Фазовый сдвиг между током и напряжением отсутствует.

Резонанс LC-цепи

Для расчета резонансной частоты колебательного контура учитывается следующее условие:

Следовательно, 2π x f x L = 1/(2πx f x C).

Отсюда получается формула резонансной частоты:

Расчет резонансной частоты, индуктивности и емкости можно сделать на онлайн калькуляторе, подставив конкретные значения.

Скорость, с которой рассеивается энергия от LC-схемы, должна быть такой же, как энергия, подаваемая на схему. Устойчивые, или незатухающие, колебания производятся электронными схемами генераторов.

LC-цепи используются либо для генерации сигналов на определенной частоте, либо для выделения частотного сигнала из более сложного. Они являются ключевыми компонентами многих электронных устройств, в частности радиооборудования, используемого в генераторах, фильтрах, тюнерах и частотных микшерах.

Свободные электрические колебания в параллельном контуре.

Основные свойства индуктивности:

— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией

. — Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Период свободных колебаний контура LC

можно описать следующим образом:

Если конденсатор ёмкостью C

заряжен до напряжения
U
, потенциальная энергия его заряда составит
. Если параллельно заряженному конденсатору подключить катушку индуктивности L
, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Что такое колебательный контур

Колебательный контур это несколько элементов в любой электрической цепи, емкость и индуктивность, которых соединены параллельно или последовательно. Для нормального функционирования колебательного контура в цепи необходим источник энергии.

Параллельный контур колебаний

При параллельном или последовательном соединениях элементов, входящих в состав электрической цепи, та или иная замкнутая проводниковая система получает одноимённое название. Явление резонанса в обоих случаях, возникает аналогичным образом, только в случае параллельного колебательного контура этот показатель относится к силе тока, а в случае с последовательным – возникает предельная частотность мгновенного изменения напряжений.

Формулы для частных случаев нахождения циклической частоты

Пружинный маятник совершает гармонические колебания с циклической частотой равной:

$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.

Гармонические колебания физического маятника происходят с циклической частотой равной:

где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.

Частным случаем физического маятника является математический маятник (физический маятник, масса которого сосредоточена в точке), циклическая частота его колебаний может быть найдена как:

где $l$ — длина подвеса, на которой находится материальная точка.

Частота колебаний в электрическом контуре равна:

где $C$ — емкость конденсатора, который входит в контур; $L$ — индуктивность катушки контура.

Если колебаний являются затухающими, то их частоту находят как:

где $\delta $ — коэффициент затухания; в случае с затуханием колебаний, $<\omega >_0$ называют собственной угловой частотой колебаний.

Как работает контур колебаний

Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.

Формула индуктивности

Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:

• Количество и расположение витков обмотки;
• Наличие или отсутствие сердечника;
• Материал сердечника.

Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.

Важно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках.

Резонансная частота. Расстройка

к оглавлению ТЭЦ ТОЭЭ к библиотеке

Превращение энергии в колебаниях Явление резонанса Резонансная частота. Расстройка Добротность колебательной системы Декремент затухания Добротность катушки индуктивности Резонанс напряжений Электромагнитный объёмный резонатор RLC-контур. Свободные колебания Реальный колебательный контур Полоса пропускания контура Магнитостатические волны Параметрические неустойчивости Нелинейный скин-эффект Диэлектрическая постоянная Дисперсия волн Диспергирующая среда Диссипативные структуры Поглощение звука Затухание колебаний Затухание контура Колебания

В цепи, содержащей реактивные элементы L и C, произойдет резонанс, если цепь имеет резистивный характер:

— угловая частота, то есть частота, приведенная к углам фазы колебаний в радианах в секунду;

, — циклическая резонансная частота, то есть частота, приведенная к циклам колебаний в секунду.

Из формулы видно, что резонанс наступает, если частота питающего генератора равна собственным колебаниям контура.

При работе с колебательным контуром необходимо знать, совпадает ли частота генератора и частота собственных колебаний контура. Если частоты совпадают, то контур остается настроенным в резонанс, если не совпадает – то в контуре присутствует расстройка.

Настроить колебательный контур в резонанс можно тремя способами:

Изменять частоту генератора при значениях емкости и индуктивности const, то есть изменяя частоту генератора мы подстраиваем эту частоту под частоту колебательного контура Изменять индуктивность катушки, при частоте питания и емкости const; Изменять емкость конденсатора , при частоте питания и индуктивности const.

Во втором и третьем способе изменяя частоту собственных колебаний контура, подстраиваем ее под частоту генератора.

При ненастроенном контуре частота генератора и контура не равны, то есть присутствует расстройка.

Расстройка – отклонение частоты от резонансной частоты.

Существует три вида расстройки:

1. Абсолютная – разность между данной частотой и резонансной
2. Обобщенная – отношение разницы реактивных сопротивлений L и C к активному R:
3. Относительная – отношение абсолютной расстройки к резонансной частоте:

При резонансе все расстройки равны нулю

, если частота генератора меньше частоты контура, то расстройка считается отрицательной; если больше – положительной.

Таким образом добротность характеризует качество контура, а обобщенная расстройка- удаленность от резонансной частоты.

Построение зависимостей X, XL, XC от f

При резонансе реактивные сопротивления равны, следовательно .

При — цепь носит емкостной характер,

— носит индуктивный характер.

Задачи

1. Сопротивление контура 15 Ом, индуктивность 636 мкГн, Емкость 600 пФ, напряжение питающей сети 1,8 В. Найти собственную частоту контура, затухание контура, характеристическое сопротивление, ток, активную мощность, добротность, напряжение на зажимах контура.

Напряжение на зажимах генератора 1 В, частота питающей сети 1 МГц, добротность 100, емкость 100 пФ. Найти: затухание, характеристическое сопротивление, активное сопротивление, индуктивность, частоту контура, ток, мощность, напряжения на емкости и индуктивности.

Тестовые задания

Отношение реактивного сопротивления к активному это :

А) Абсолютная расстройка;

Б) Обобщенная расстройка;

В) Относительная расстройка.

к оглавлению ТЭЦ ТОЭЭ к библиотеке
Знаете ли Вы,

что такое мысленный эксперимент, gedanken experiment? Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, «мысленный эксперимент» фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей «мысленных экспериментов» является обман слушателя или читателя путем замены настоящего физического эксперимента его «куклой» — фиктивными рассуждениями под честное слово без самой физической проверки. Заполнение физики воображаемыми, «мысленными экспериментами» привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие «фантики» от настоящих ценностей. Релятивисты и позитивисты утверждают, что «мысленный эксперимент» весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении. Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: «Если факт не соответствует теории — измените факт» (В другом варианте » — Факт не соответствует теории? — Тем хуже для факта»). Максимально, на что может претендовать «мысленный эксперимент» — это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте. Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем. Понятие «мысленный эксперимент» придумано специально спекулянтами — релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим «честным словом». Подробнее читайте в FAQ по эфирной физике.

Как правильно рассчитать частоту контура колебаний

Для последовательного колебательного контура добротность растет с увеличением значения индуктивности. Таким образом, при расчетах элементов, следует учитывать величину добротности. Также, необходимо иметь в виду, что емкости конденсаторов выбираются из стандартного ряда значений, и на этом основании изготавливается катушка индуктивности.

Явление резонанса позволяет использовать колебательные контуры в качестве частотно зависимых цепей и в элементах фильтров. Радиоприемные устройства наиболее широко используют избирательные свойства колебательных систем. Если вместо емкости использовать кварцевый резонатор, то можно получить электрическую цепь с катушкой индуктивности, обладающей очень высокой добротностью. Такие схемы широко используются в задающих генераторах, где требуется высокая точность для определения периода изменения направления частиц.

Определение и формула циклической частоты колебаний

Определение Циклическая частота — это параметр, характеризующий колебательные движения. Обозначают эту скалярную величину как $\omega $, иногда $<\omega >_0$.
Напомним, что уравнение гармонических колебаний параметра $\xi $ можно записать как:

где $A=<\xi >_$ — амплитуда колебаний величины $\xi $; $\left(<\omega >_0t+<\varphi >_0\right)$=$\varphi $ — фаза колебаний; $<\varphi >_0$ — начальная фаза колебаний.

Циклическую частоту при гармонических колебаниях определяют как частную производную от фазы колебаний ($\varphi $) по времени ($t$):

Циклическая частота колебаний связана с периодом ($T$) колебаний формулой:

Циклическую частоту с частотой $?$$?$ связывает выражение:

Источник